四边形对角互补吗

在讨论四边形对角的之前,我们先来了解一些基本概念。
什么是四边形?
在同一平面内,由不在同一直线上的四条线段首尾顺次相接的图形叫做四边形。
四边形四个内角之间有什么关系呢?
四边形的内角和定理:四边形的内角和等于360°。
三角形的三边如果确定后,它的形状、大小就确定了,这是三角形的稳定性。但是四边形的四边确定后,它的形状不能确定,可以变动,这就是四边形所具有的不稳定性。
因此,一般情况下,四边形的内角和等于360°,但对角和就不一定等于180°。
什么时候四边形的对角能互补呢?当这个四边形为圆内接四边形的时候,四边形的对角能互补。
什么是圆内接四边形?
四边形的所有顶点都在同一个圆上,这个四边形叫圆内接四边形,这个圆叫这个四边形的外接圆。
定理:圆的内接四边形的对角互补,并且任何一个外角都等于它的内对角。
下面让一起来简单证明一下这个定理,如图所示。
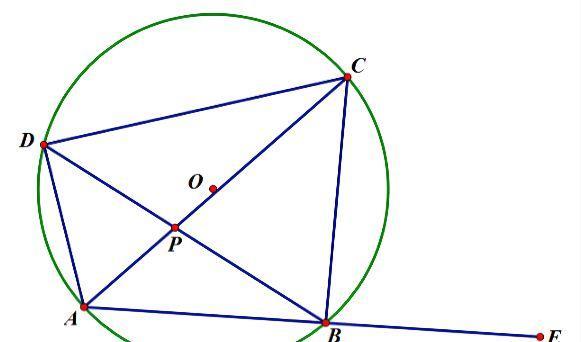
∵∠BAD为优弧BCD所对的圆周角,∠DCB为弧BD所对的圆周角。
优弧BCD+弧BD=360°
∴2∠BAD+2∠DCB=360°
∴∠BAD+∠DCB=180°
同理可的∠ABC+∠ADC=180°.
因此,我们就可以得到圆的内接四边形的对角互补。
另外,∠ABC+∠CBE=180°
所以∠CBE=∠ADC,即圆内接四边形的任意一个外角等于它的内对角。
圆内接四边形知识点总结:
1、圆内接四边形的对角互补:∠BAD+∠DCB=180°,∠ABC+∠ADC=180°;
2、圆内接四边形的任意一个外角等于它的内对角:∠CBE=∠ADC;
3、圆心角的度数等于所对弧的圆周角的度数的两倍:∠AOB=2∠ACB=2∠ADB;
4、同弧所对的圆周角相等:∠ABD=∠ACD;
5、圆内接四边形对应三角形相似:△ABP∽△DCP(三个内角对应相等)。
典型例题分析1:
已知如图,在圆内接四边形ABCD中,∠B=30°,则∠D=.
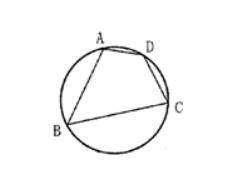
解:∵圆内接四边形ABCD中,∠B=30°,
∴∠D=180°﹣30°=150°.
故答案为:150°.
考点分析:
圆内接四边形的性质。
题干分析:
根据圆内接四边形对角互补,直接求出即可.
解题反思:
此题主要考查了圆内接四边形的性质,灵活应用圆内接四边形的性质是解决问题的关键.
典型例题分析2:
如图,梯形ABCD内接于⊙O,AD∥BC,∠DAB=49°,则∠AOC的度数为.
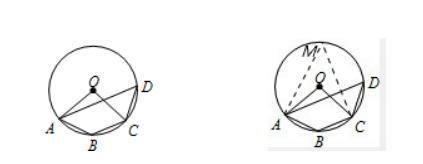
解:如图,在弧AD上取点M,连接AM,CM,
∵AD∥BC,∠DAB=49°,
∴∠ABC=131°,
∴∠M=49°,
∠AOC=98°.
故答案为:98°.
考点分析:
圆周角定理;平行线的性质。
题干分析:
如图,在弧上取点M,连接AM,CM,根据题意推出∠AMC,然后根据圆的内接四边形的性质,推出∠ABC的度数,随即可求出∠M的度数,即可推出∠AOC的度数.
解题反思:
本题主要考查圆周角定理、圆的内接四边形的性质、平行线的性质,关键在于做好辅助线,求得∠M的度数。