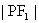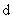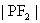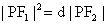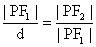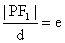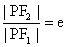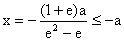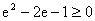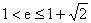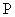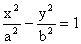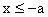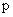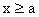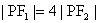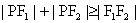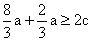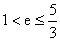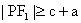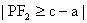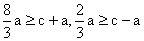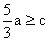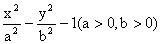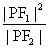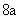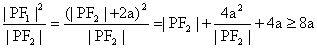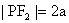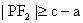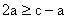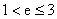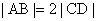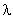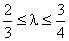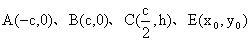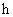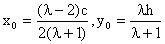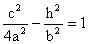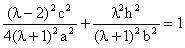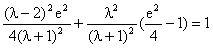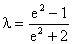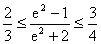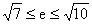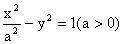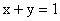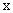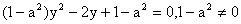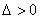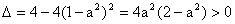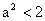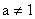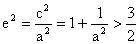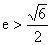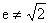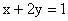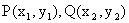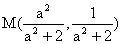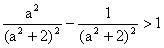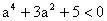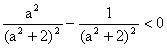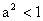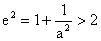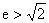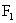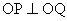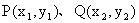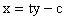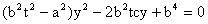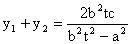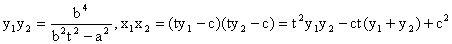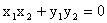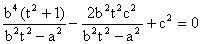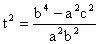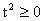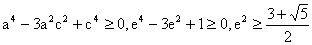高中数学:求双曲线离心率的取值范围

求双曲线离心率的取值范围涉及到解析几何、平面几何、代数等多个知识点,解题关键是挖掘题中的隐含条件,构造不等式,下面举例说明。
一、利用双曲线性质
例1、设点P在双曲线的左支上,双曲线两焦点为,已知
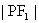
是点P到左准线的距离
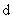
和
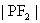
的比例中项,求双曲线离心率的取值范围。
解析:由题设
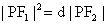
得:
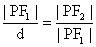
。由双曲线第二定义
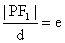
得:
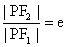
,由焦半径公式得:

,则
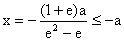
,即
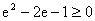
,解得
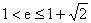
。
小结:求双曲线离心率取值范围时可先求出双曲线上一点的坐标,再利用性质:若点
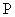
在双曲线
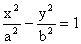
的左支上则
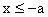
;若点
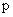
在双曲线的右支上则
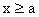
。
二、利用平面几何性质
例2、设点P在双曲线的右支上,双曲线两焦点,
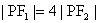
,求双曲线离心率的取值范围。
解析:由双曲线第一定义得:

,与已知联立解得:

,由三角形性质
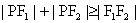
得:
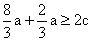
解得:
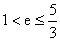
。
小结:求双曲线离心率的取值范围时可利用平面几何性质,如“直角三角形中斜边大于直角边”、“三角形两边之和大于第三边”等构造不等式。
三、利用数形结合
例3、(同例2)
解析:由例2可知:
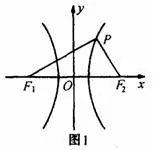
,点P在双曲线右支上由图1可知:
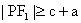
,
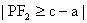
,即
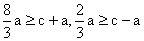
,两式相加得:
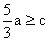
,解得:。
四、利用均值不等式
例4、已知点在双曲线
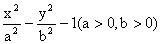
的右支上,双曲线两焦点为,
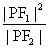
最小值是
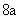
,求双曲线离心率的取值范围。
解析:
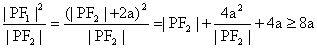
,由均值定理知:当且仅当
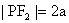
时取得最小值,又
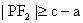
所以
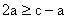
,则
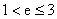
。
五、利用已知参数的范围
例5、已知梯形ABCD中,
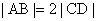
,点E分有向线段
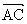
所成的比为
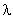
,双曲线过C、D、E三点,且以A、B为焦点,当
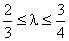
时,求双曲线离心率的取值范围。
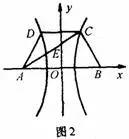
解析:如图2建立平面直角坐标系,设双曲线方程为,设
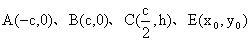
其中
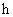
是梯形的高,由定比分点公式得
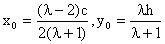
,把C、E两点坐标分别代入双曲线方程得
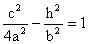
,
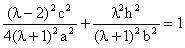
,两式整理得
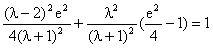
,从而建立函数关系式
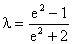
,由已知得,
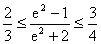
,解得
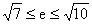
。
六、利用直线与双曲线的位置关系
例6、已知双曲线
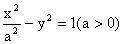
与直线:
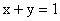
交于P、Q两个不同的点,求双曲线离心率的取值范围。
解析:把双曲线方程和直线方程联立消去
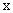
得:
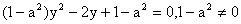
时,直线与双曲线有两个不同的交点则
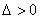
,
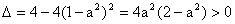
,即
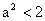
且
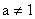
,所以
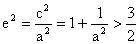
,即
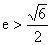
且
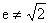
。
七、利用点与双曲线的位置关系
例7、已知双曲线上存在P、Q两点关于直线
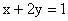
对称,求双曲线离心率的取值范围。
解析:设
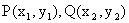
,弦PQ中点为M,由点差法求得
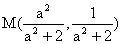
,当点M在双曲线内部时
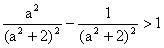
,整理得:
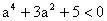
无解;当点M在双曲线外部时,点M应在两渐近线相交所形成的上下区域内,由线性规划可知:
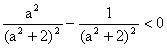
,即
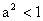
,则
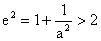
,所以
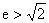
。
八、利用非负数性质
例8、已知过双曲线左焦点
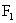
的直线交双曲线于P、Q两点,且
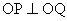
(

为原点),求双曲线离心率的取值范围。
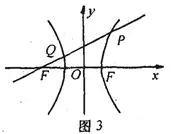
解析:设
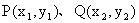
,过左焦点的直线方程:
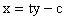
,代入双曲线方程得:
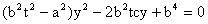
,由韦达定理得:
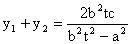
,
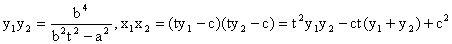
,由OP⊥OQ得
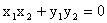
,即:
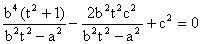
,解得:
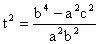
,因为
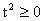
,所以

,则
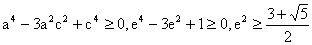
,所以
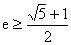
。
求双曲线离心率的取值范围时要根据题情,因题制宜挖掘题中隐含的不等关系,构造不等式,从而求出双曲线离心率的取值范围。
--END--


标签:

180
余美颜:为报复父亲和男性,4年交往3000男友,临终遗言很虐心 在现代社会,穿泳衣、交往男友、行为大胆等都是可以被世俗容纳的,不越线的个人作风。但是倒退百年, 在那个西方思...

104
推荐十本高分榜玄学类女强小说 第一本:《神算萌妻,她马甲飒爆了》作者:易升 书籍简介 秦家富可敌国,独子秦北也天纵奇才,美貌妖孽,却是生来命里带煞,任何与他接触的女人...
120
干货来袭:教师联欢会小品剧本《新闻联播》 《新闻联播》 一、形式:小品 二、作者:永不言弃向前进 三、小品剧本: 《新闻联播》 -----------三八人民电视台 甲:亲爱的观众朋友们...

91
辛巴下跪宣布复出:为了捞钱,拼了 2020年12月,某手平台最厉害的带货主播辛巴出事了。 起因是闹得沸沸扬扬的“假燕窝”事件。 原本以为这样的主播会被抵制封杀,毕竟他打着为了...
74
德国货币马克 1948年6月20日德国西占区实行货币改革,并发行联邦德国马克,正式取代1924-1948年通行的帝国马克(Reichs Mark)。两德统一后,1990年7月1日起,通行全国。辅币是芬尼(Pf...

179
日本不顾全球强烈反对,将核废水排入海洋,如今惨遭现世报! 日本不顾全人类强烈反对,执意将核废水排入海洋,现在报应来了!就在本月,日本东京电力公司开始向福岛第一核电站...

163
甘肃名城酒泉市 说到甘肃省酒泉,你首先想到哪里?也许大多数人都会想到酒泉卫星发射中心,不过有意思的是,这个叫做酒泉的卫星发射中心其实从来都不在酒泉,而在内蒙古阿拉善...

201
东北头号杀手莫磊,身扛“过肩龙”称霸东北十余年,近况令人唏嘘 1996年上映的黑帮电影《古惑仔》中,郑伊健饰演的“陈浩南”身体上有一条从胸部延伸至右臂的龙形纹身,这个帅...

88
推荐十部全球公认最好看电影 1、 肖申克的救赎 《肖申克的救赎》是由弗兰克·达拉邦特执导,蒂姆·罗宾斯、摩根·弗里曼等主演。该片改编自斯蒂芬·金《四季奇谭》中收录的同名小...

102
26岁台湾女作家林奕含之死:无边界的宽容大度真会害死人啊 01. 26岁台湾女作家林奕含,自杀于2017年4月27日,她的死当时引起了轰动,背后的真正原因令人极其愤慨:她死于少年时补课...

62
美国的地理环境有哪些优势和劣势 人没办法选择自己的父母和出身,国家也同样有自己无法选择的东西。比如一个国家的地理位置就是天然注定的。地理环境虽无法选择,但并不存在绝...

114
阎维文的人生经历 在阅读此文之前,麻烦您点击一下“关注”,既方便您进行讨论和分享,又能给您带来不一样的参与感,感谢您的支持。 文|艺术家 编辑|它家的猫 近年来,娱乐圈“...

186
马丕瑶审案 马丕瑶审案 马丕瑶(1831~1895) [1] ,字玉山,清代广东巡抚。河南安阳县蒋村人。清同治元年(1862)进士。历任山西平陆县、永济县知县,解州(今山西运城)、辽州(今山西...

74
凤翅镏金镗难敌擂鼓瓮金锤的宿命,在数百年后终于扳回一局 #文章首发挑战赛# 项羽的槟铁镀铜枪造就了西楚霸王的威名,关云长的青龙偃月刀书写了关圣帝的传奇,画杆方天戟展现了...

159
透过《维荣之妻》、《斜阳》,浅谈二战后日本女性意识的觉醒 日本作家太宰治的《维荣之妻》、《斜阳》以日本二战后初期的社会环境为故事背景,从女性视角分别叙述了女主人公各...

116
唐山孤竹国酒业的由来 创始年代与传承关系 清朝雍正年间(1728年)杨之荣在新寨创立杨氏福泉烧锅,经六代传承,到1898年传至第八代杨荣兴(杨之荣首传给孙辈)。乐亭县解放后经过...

150
潘石屹,一夜回到解放前 作者:张生 来源:鸣金网(ID:mingjin-wang) (本文首发:鸣金网,图片来源:网络) 跑路失败的潘石屹,很难笑得出来了。 乖乖认罚的“笑面虎”,苦日子可...

148
陕西省8所211、3所985大学介绍与排名 01 什么是211、985工程 “211工程”是中国政府实施“科教兴国”战略的重大举措,是中华民族面对世纪之交的中国国内外形势而作出的发展高等教育的...

87
从“清华才子”到“千夫所指”,高晓松终究活成了一个“笑话” 在阅读此文之前,麻烦您点击一下“关注”,既方便您进行讨论和分享,又能给您带来不一样的参与感,感谢您的支持...

148
富瀚微电子:聚专业人才,做安防监控芯片领域领军者 2004年2月14日,情人节,一群怀揣着梦想的“小伙伴”从深圳来到上海,创立了上海富瀚微电子有限公司。用公司总工程师万建军...